Newton's Method

A useful method of determining roots of functions is Newton-Raphson Method (Raphson simplified Newton's Method). This can be scaled up to do many problems: determine the square root of x, find the intersection of two functions, and as stated before, finding the roots of a polynomial.

How does this work?

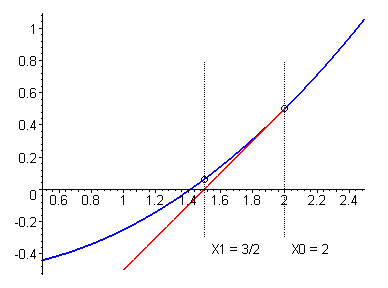
The premise of Newton's Method is you make a guess: in this case, you guess that the root of x^2 is 2. Then, you take the line tangent to the function at that point, and find the x-intercept of that line. Then, you take the line tangent to the function at that point, or in this case, 1, and you do the same thing over and over again.

Generalize

So let's say you have a function f(x), and a derivative f'(x). So, you begin with a guess c.

So the tangent line to that is

y - f(c) = f'(c)(x - c).

We want y = 0, because we want the x intercept

0 - f(c) = f'(c)(x - c)

-f(c)/f'(c) = x - c

c - f(c)/f'(c) = x

You can keep repeating that, so you can generalize it as

x_n+1 = x_n - f(x_n)/f'(x_n)

Example for x^2 = 0

x₁ = 2

x₂ = 2 - f(2)/f'(2) = 2 - 4/4 = 1

x₃ = 1 - f(1)/f'(1) = 1 - 1/2 = 1/2

x_n+1 = x_n - (x_n)^2/(2x_n) =

x_n - x_n/2 = x_n/2

2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, -> 0

This is a bad example, because it takes an infinite number of iterations, but it also the simplest case. This is a very accurate way of determine a root of a function, although there are also many cases it doesn't work. 

Find the square root of a number

Let's say you want to find the square root of 3

x = √3, or x^2 = 3, which equals x^2 - 3 = 0

Guess: 2

x₁ = 2 - f(2)/f'(2) = 2 - 1/4 = 1.75

x₂ = 1.75 - f(1.75)/f'(1.75) = 1.75 - 0.0625/3.5 = 1.73214

x₃ = 1.73214 - f(1.73214)/f'(1.73214) = 1.73214 - 0.00017/3.4642 = 1.73209

1.73209² = 3.000138

So, in 3 iterations, it gets the result accurate to four decimal places (real square root of 3 = 1.73205). 

In Python

def sqrt(n, iterations = 10):
    guess = n/2 #arbitrary guess
    f = lambda x: x ** 2 - n
    fprime = lambda x: 2 * x
    for i in range(iterations):
        guess = guess - f(guess)/fprime(guess)
    return guess

Comparison with math.sqrt(n)

>>> import math
>>> math.sqrt(17.5)
    4.183300132670378
>>> sqrt(17.5, 6) #our square root function
    4.183300132670378
    

In only 6 iterations, the Newton-Raphson method found the result accurate to 15 decimal places! 

A Failure

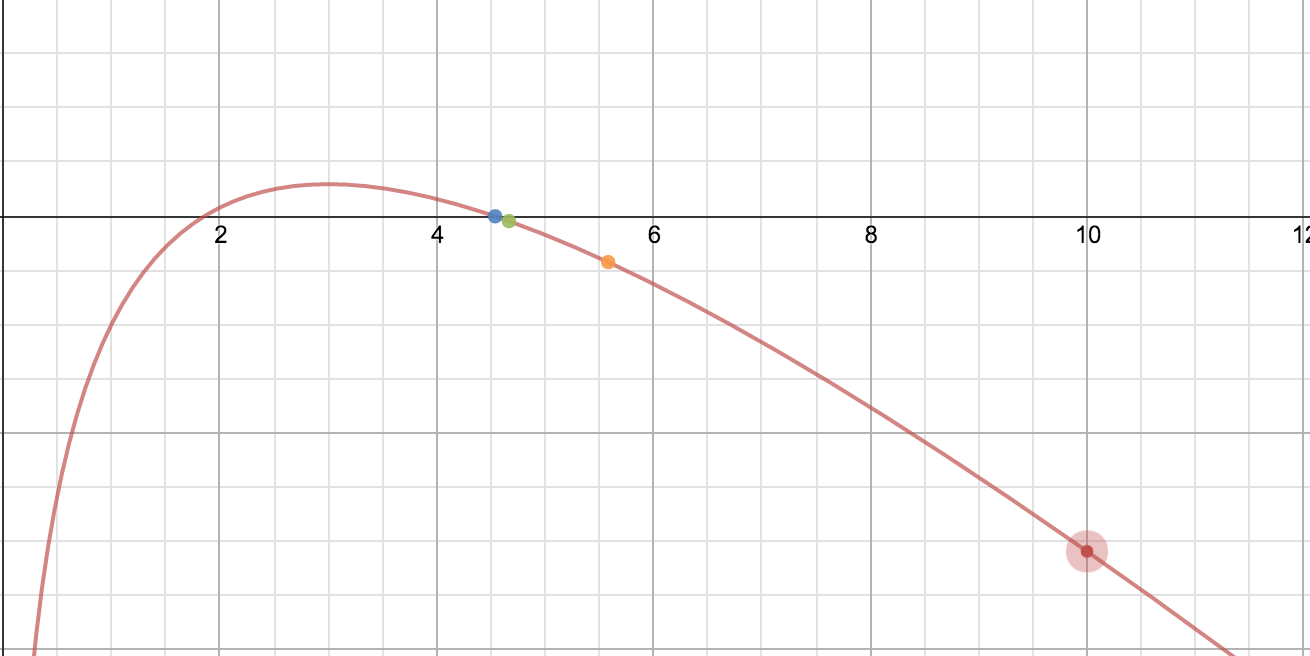
ln(x)

Order of the points being red -> orange -> green -> blue (order of the rainbow)

It breaks after the first iteration

When the original guess = 2, it works fine, converging to 1 very quickly. After 3 iterations, the result is 0.996.

When the original guess = 2.5, it takes one more additional iteration to get to 0.991. This is still good, but it's getting worse. 

When you start x at 3, the tangent line hits at a negative value. Why does this happen though?

When you look at the formula for determining the next point, it's

x_{n + 1} = x_n - ln(x_n)/(1/x_n) = x_n - x_n* ln(x_n)
OR

x_n+1 = x_n(1 - ln(x_n)).

x_n+1 must be positive, so ln(x_n) < 1. If the guess is ≥e, the next guess will be < 0, and Newton's Method will fail.

Real-Life Applications

Find ln(n)

Although ln(x) broke at various points, if you do ln(n) = x -> e^x = n -> e^x - n = 0

Intersection of Two Functions

Here, the function is f(x) = e^x - 1. In only four iterations, it found that it was 0.

Let's say 3ln(x) = x.  In order to solve that equation, you need some complicated math (maybe Lambert W-Function, I'm not positive). Using Newton's method, you find the zeroes of f(x) = 3ln(x) - x after four iterations. Obviously, the only solutions are positive, because ln(x) has a domain of all positive numbers. So Newton's method for this problem works for every number > 0 except for 3, because f'(x) = 3/x - 1. So, f'(3) = 0, and Newton's method would break if the initial guess is 3.  This becomes so linear that even when x = 5000, after 3 iterations, the result becomes 5, which is pretty close to 4.536.

Approximate results for ugly values 

Let's say you know sqrt(16) = 4, and you want to find out what sqrt(16.001). You just do Newton's method for x^2 - 16.001, with 4 being the first guess. 

Overall, Newton's Method is an extremely useful method of approximating roots of functions, and although it breaks down in special cases, it is invaluable in math and real life. 

NOTE:  This is a more rigorous and updated form of this post: How does the square root function work?